【導(dǎo)讀】所有的聲音均是由一系列不同頻率的聲信號(hào)混合而成，如果可以人為地生成一種聲音，其頻率與所要消除的噪聲完全一樣，只是相位與之相反就可以將這噪聲完全抵消掉。主動(dòng)噪聲控制(ANC) 就是在設(shè)備中加入了對(duì)噪聲分析的電路，并通過(guò)控制器快速運(yùn)算分析，產(chǎn)生可以抵消外界噪聲的人為聲信號(hào)，通過(guò)揚(yáng)聲器將相反相位的信號(hào)播放后抵消目標(biāo)噪聲。
0 引言
所有的聲音均是由一系列不同頻率的聲信號(hào)混合而成，如果可以人為地生成一種聲音，其頻率與所要消除的噪聲完全一樣，只是相位與之相反就可以將這噪聲完全抵消掉。主動(dòng)噪聲控制(ANC) 就是在設(shè)備中加入了對(duì)噪聲分析的電路，并通過(guò)控制器快速運(yùn)算分析，產(chǎn)生可以抵消外界噪聲的人為聲信號(hào)，通過(guò)揚(yáng)聲器將相反相位的信號(hào)播放后抵消目標(biāo)噪聲。ANC 可用于多種應(yīng)用，包括個(gè)人聽(tīng)力設(shè)備[1-2]，管道和室內(nèi)聲學(xué)增強(qiáng)，發(fā)動(dòng)機(jī)排氣噪聲抑制以及改善車(chē)輛外殼風(fēng)噪，飛機(jī)艙和振動(dòng)機(jī)器中的聲學(xué)[3-4]。隨著現(xiàn)代工業(yè)的飛速發(fā)展，大部分工業(yè)設(shè)備的功率越來(lái)越大，轉(zhuǎn)速越來(lái)越快，噪聲危害也日益突出。噪聲不僅影響產(chǎn)品質(zhì)量、操作精度、縮短產(chǎn)品壽命、危及安全性，且污染環(huán)境、影響人生健康。因此，掌握噪聲控制技術(shù)是工業(yè)發(fā)展面臨的重大課題。
在實(shí)際研究應(yīng)用中，濾波x 最小均方算法(filteredx LMS, FxLMS)[5] 結(jié)構(gòu)簡(jiǎn)單、算法穩(wěn)定，所以FxLMS算法在ANC 控制器中使用最為廣泛；還有改進(jìn)而成的歸一化LMS[6]，其穩(wěn)態(tài)誤差可以降低到很小，但是收斂速度會(huì)受到很大影響；基于Sigmoid 函數(shù)的SVSLMS[7]算法也被廣泛應(yīng)用，其收斂速度較快但是穩(wěn)態(tài)誤差又達(dá)不到要求。此類(lèi)變步長(zhǎng)控制算法[8-11] 的主要問(wèn)題在于算法中收斂步長(zhǎng)多數(shù)是反饋誤差信號(hào)的函數(shù)。經(jīng)濾波器迭代計(jì)算后，該信號(hào)收斂不為零，會(huì)致使系統(tǒng)出現(xiàn)非零失調(diào)問(wèn)題，則容易導(dǎo)致系統(tǒng)進(jìn)入穩(wěn)態(tài)后的誤差仍然較大，且不再收斂。因此通過(guò)構(gòu)建前饋信號(hào)的相關(guān)函數(shù)為參考的變步長(zhǎng)主動(dòng)噪聲控制系統(tǒng)，來(lái)提高低頻噪聲降噪效果成為了可行的方向。
在自由場(chǎng)中，單通道主動(dòng)噪聲控制系統(tǒng)產(chǎn)生的“消音區(qū)”的直徑約為控制聲波波長(zhǎng)的1/10[12]，也就是說(shuō)常規(guī)單通道主動(dòng)控制系統(tǒng)的有效范圍只有直徑二三十厘米，這對(duì)于實(shí)際應(yīng)用來(lái)說(shuō)是遠(yuǎn)遠(yuǎn)不夠的。因此大區(qū)域噪聲主動(dòng)控制需要使用多通道控制算法來(lái)實(shí)現(xiàn)[13-17]，為此本文提出一種基于可變步長(zhǎng)的多通道主動(dòng)控制算法，并利用仿真實(shí)驗(yàn)驗(yàn)證其可行性。
1 控制算法
1.1 可變步長(zhǎng)
當(dāng)采用定收斂步長(zhǎng)時(shí)，系統(tǒng)的收斂精度和收斂時(shí)間呈現(xiàn)出對(duì)立的情況，即收斂步長(zhǎng)設(shè)置較小時(shí)，收斂精度更高，但是收斂時(shí)間卻大大延長(zhǎng)；反之，收斂步長(zhǎng)設(shè)置較大時(shí)，收斂時(shí)間減小，但是收斂精度大為降低。因此，
為了消除定收斂步長(zhǎng)FxLMS 的局限性，考慮采用可變收斂步長(zhǎng)FxLMS 算法。
基于Sigmiod 函數(shù)的可變收斂步長(zhǎng)算法(SVSLMS) 中
由式(1) 知，可變收斂步長(zhǎng)μ(n) 是e(n) 的Sigmiod函數(shù)。初始收斂時(shí)，誤差較大則收斂因子取值也較大；隨著誤差的逐漸變小，則收斂因子取值也隨之變小。從而同時(shí)滿(mǎn)足了自適應(yīng)濾波的準(zhǔn)則：較快的收斂速度、跟蹤速度以及較小的穩(wěn)態(tài)誤差。但此式計(jì)算時(shí)較為繁瑣，同時(shí)誤差e(n) 在0 附近的穩(wěn)定性不夠理想，易引起非零失調(diào)。歸一化LMS 算法中可變步長(zhǎng)用參考輸入信號(hào)的功率值進(jìn)行歸一化處理，從而得到與參考輸入信號(hào)功率有關(guān)的可變收斂步長(zhǎng)μ。可變收斂因子函數(shù)表示為：
由于x(n) 的歐式平方范數(shù)的硬件實(shí)現(xiàn)較為復(fù)雜，且參考輸入信號(hào)只取當(dāng)前瞬時(shí)值，x(n) 的歐式平方范數(shù)即等于x(n) 的絕對(duì)值平方，即改進(jìn)為：
其中，|x(n)|2 是第n 次迭代中的瞬時(shí)參考輸入信號(hào)的平方值。由式(1)、式(3) 可知，將可變收斂因子的計(jì)算中由原求解輸入向量的自相關(guān)矩陣的運(yùn)算，變換為標(biāo)量的平方值運(yùn)算，可提高收斂性，故令：
為改善非零失調(diào)的問(wèn)題，將可變步長(zhǎng)的輸入信號(hào)改為系統(tǒng)參考信號(hào)的變化量，可得
1.2 多通道可變步長(zhǎng)
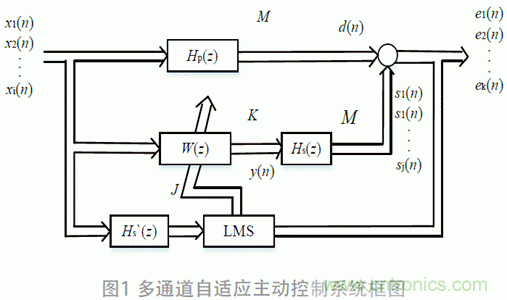
MIMO 濾波-x LMS 算法是應(yīng)用最為廣泛的噪聲控制算法，系統(tǒng)框圖如圖1 所示。設(shè)系統(tǒng)中有I 個(gè)參考傳感器，J 個(gè)次級(jí)揚(yáng)聲器，K 個(gè)誤差傳感器。IJ 個(gè)自適應(yīng)濾波器采用橫向?yàn)V波器，其長(zhǎng)度為L(zhǎng)，濾波器權(quán)系數(shù)采用矢量形式統(tǒng)一表示為W(z)。Hp(z) 代表IK 個(gè)初級(jí)通路的傳遞函數(shù)，Hs(z) 代表JK 個(gè)次級(jí)通路的傳遞函數(shù)，Hs`(z) 是次級(jí)通路傳遞函數(shù)的估計(jì)值。初級(jí)通路和次級(jí)通路等效為FIR 濾波器，假設(shè)其長(zhǎng)度分別為L(zhǎng)p 和Ls。
設(shè)xi(n) 為第i 個(gè)參考傳感器在第n 時(shí)刻的輸入信號(hào)，稱(chēng)為第i 個(gè)參考信號(hào)，即為xi(n)=[xi(n), xi(n-1),…,xi(n-L+1)]T；yj(n) 為第j 個(gè)控制器在第n 時(shí)刻的輸出信號(hào)， 表示為y(n) = [y1(n), y2(n),…, yJ(n)]T；dk(n) 為第k 個(gè)誤差傳感器處第n 時(shí)刻的期望信號(hào)，表示為d(n) = [d1(n), d2(n),…, dK(n)]T；ek(n) 為該處第n 時(shí)刻的誤差項(xiàng)信號(hào)表示為e(n) = [e1(n), e2(n),…, eK(n)]T。
則第j 個(gè)揚(yáng)聲器的輸出信號(hào)即為sj(n) = yj(n)×Hs(n)。誤差信號(hào)矢量可寫(xiě)成
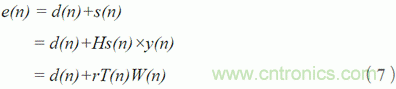
式中：Hs(n) 為K×J 階次級(jí)通路脈沖響應(yīng)矩陣，第(k，j)元素為hskj(n)；r(n) 為J×KLs 階濾波 -x 信號(hào)矩陣，其(j，k) 元素為
設(shè)多通道自適應(yīng)主動(dòng)控制系統(tǒng)的目標(biāo)函數(shù)為
與常用FxLMS 算法類(lèi)似，利用最陡下降法原理，可以推導(dǎo)出控制器權(quán)系數(shù)迭代公式為
w(n +1) = w(n)−2μr(n)e(n) （10）
整個(gè)算法表達(dá)式總結(jié)如式(11)~(13) 所示
第k 個(gè)誤差傳感器接收到的信號(hào)為
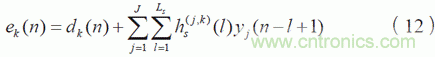
第i 個(gè)參考傳感器至第j 個(gè)控制器的權(quán)系數(shù)迭代公式
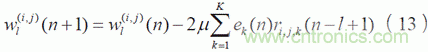
式中
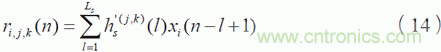
其中μ 為收斂步長(zhǎng)，可由式(5) 得到。則此算法命名為可變步長(zhǎng)多通道濾波x 最小均方算法(VM-FxLMS)。
2 仿真實(shí)驗(yàn)
2.1 單通道算法性能
在MATLAB 中建立ANC 系統(tǒng)模型，信號(hào)模擬排風(fēng)扇噪聲。風(fēng)扇噪聲由旋轉(zhuǎn)噪聲和絮流噪聲組成，旋轉(zhuǎn)噪聲用正弦信號(hào)代表，頻率為500 Hz 左右，絮流噪聲用白噪聲代表，截至頻率為4 kHz。在系統(tǒng)中加入低通濾波器，將高于4 kHz 的噪聲濾除。
下面將分別使用FxLMS 算法、歸一化NLMS 算法、SVSLMS 算法和本文提出的單VM-FxLMS 算法針對(duì)此模擬噪聲進(jìn)行測(cè)試對(duì)比。三種算法初始收斂步長(zhǎng)μ 均設(shè)為0.01。仿真測(cè)試結(jié)果如圖2 所示。
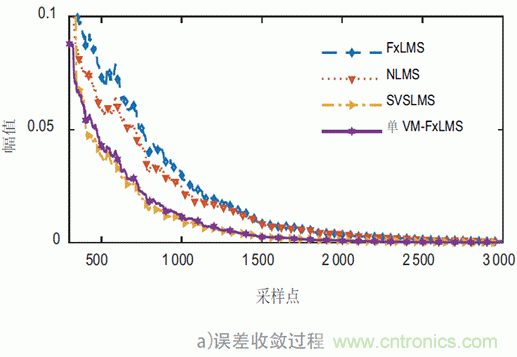
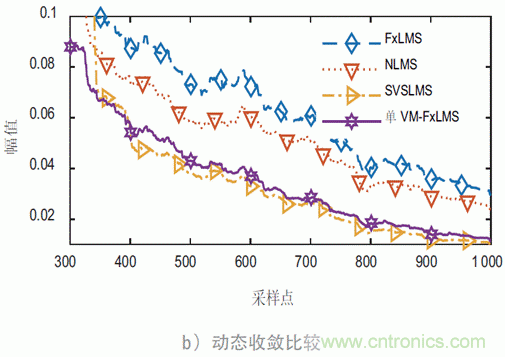
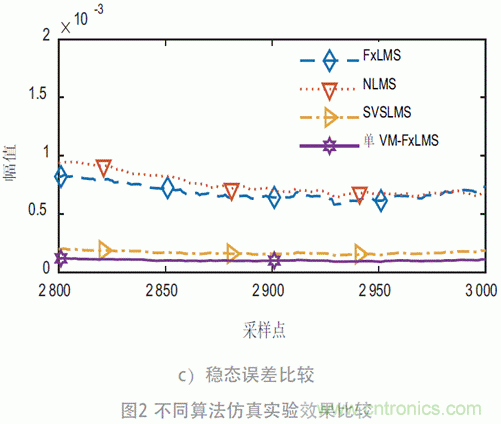
初始收斂狀態(tài)時(shí)，從圖2 a) 和b) 可看出，可變步長(zhǎng)算法的收斂速度比定步長(zhǎng)算法有著明顯優(yōu)勢(shì)。本文提出的單VM-FxLMS 算法的收斂速度很快，且在其他算法趨于穩(wěn)定時(shí)本算法還能夠進(jìn)一步收斂。在穩(wěn)態(tài)階段，從圖2 c) 中可看出，單VM-FxLMS 算法穩(wěn)態(tài)誤差最低，且平穩(wěn)無(wú)明顯波動(dòng)。從此仿真結(jié)果可看出，本文所提出的算法優(yōu)于傳統(tǒng)的定步長(zhǎng)FxLMS 算法和一些其他的變步長(zhǎng)算法。
2.2 多通道區(qū)域降噪實(shí)現(xiàn)
在MATLAB 中模擬4 m×4 m 大小的區(qū)域，在區(qū)域內(nèi)設(shè)置多個(gè)噪聲源，噪聲成分同2.1 節(jié)所設(shè)噪聲源且增加更多的干擾。初始收斂步長(zhǎng)μ 均設(shè)為0.01，多通道ANC 系統(tǒng)設(shè)置為16 通道。在此區(qū)域降噪前和降噪后的噪聲仿真圖如圖3 所示。
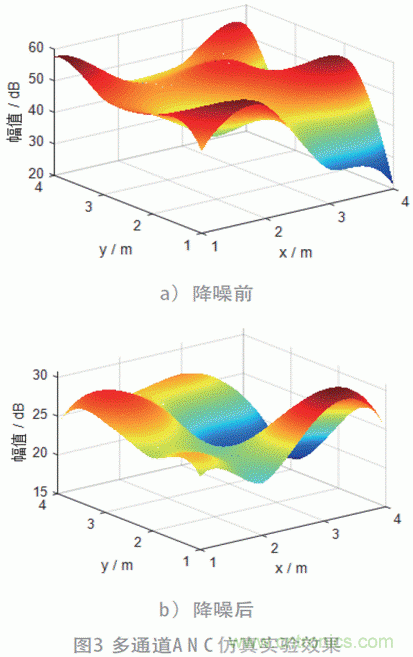
如圖3 a) 所示，此區(qū)域中平均噪聲約為50 dB，最高點(diǎn)噪聲約為60 dB。降噪后的仿真圖如圖3 b) 所示，除個(gè)別點(diǎn)之外，整個(gè)區(qū)域的噪聲有非常明顯的降低，平均剩余噪聲約為25 dB。降噪后相比于降噪前，噪聲降低了約25 dB，個(gè)別區(qū)域是有噪聲升高的現(xiàn)象。此仿真實(shí)驗(yàn)表明，本文提出的多通道ANC 系統(tǒng)對(duì)區(qū)域降噪具有非常好的控制些效果。
3 結(jié)語(yǔ)
本文提出的基于可變步長(zhǎng)的多通道噪聲主動(dòng)控制方法以參考信號(hào)的變化量作為可變步長(zhǎng)函數(shù)的輸入信號(hào)，能夠改善算法非零失調(diào)的狀況，對(duì)比于其他常用的控制算法，在收斂速度與收斂效果上有明顯優(yōu)勢(shì)。然后將可變步長(zhǎng)算法擴(kuò)展至多通道主動(dòng)控制算法，對(duì)于大區(qū)域的噪聲控制的仿真當(dāng)中，多通道ANC 系統(tǒng)表現(xiàn)出了非常好的降噪效果。同時(shí)，多通道ANC 系統(tǒng)的計(jì)算量是一個(gè)需要進(jìn)一步研究的重點(diǎn)，這也是未來(lái)研究工作的重點(diǎn)。
免責(zé)聲明：本文為轉(zhuǎn)載文章，轉(zhuǎn)載此文目的在于傳遞更多信息，版權(quán)歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權(quán)問(wèn)題，請(qǐng)電話(huà)或者郵箱聯(lián)系小編進(jìn)行侵刪。
