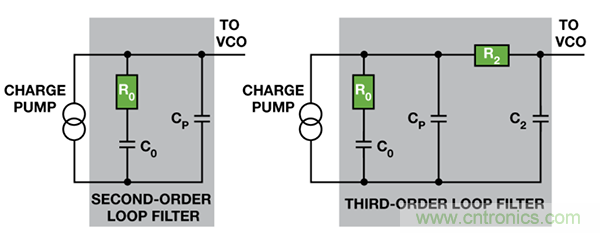
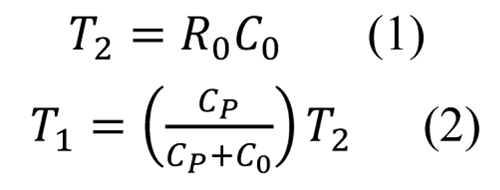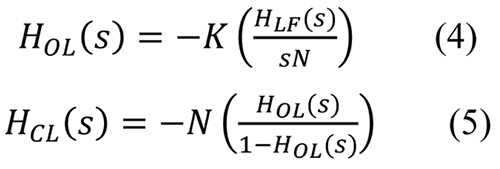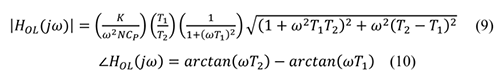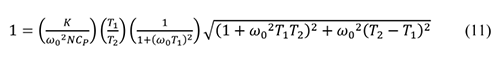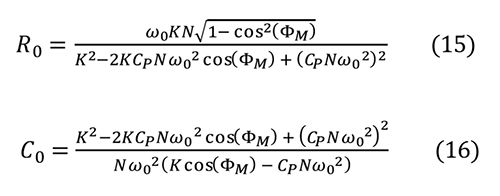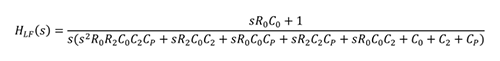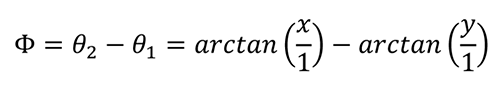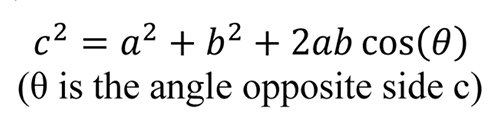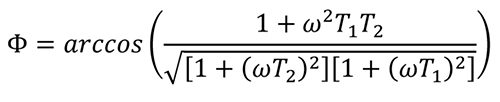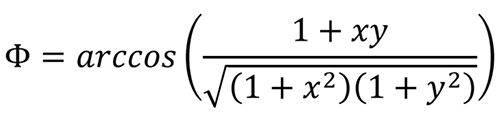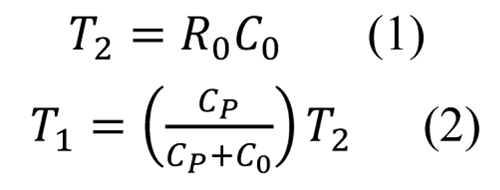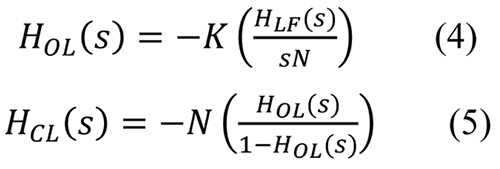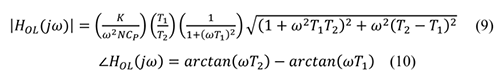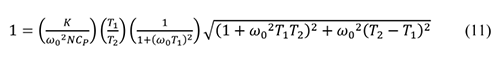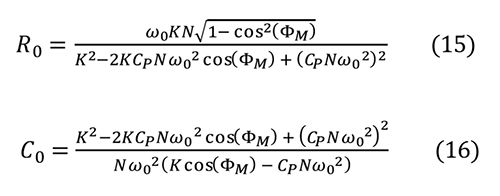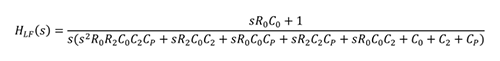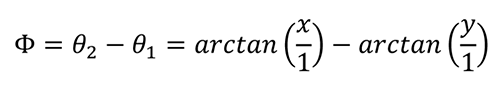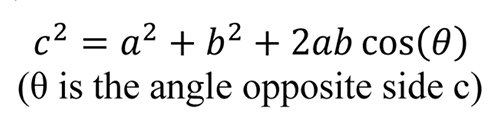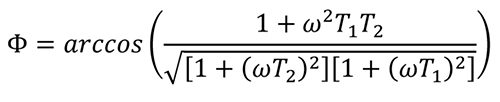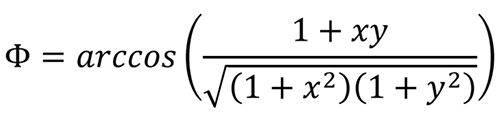【導(dǎo)讀】如參考文獻(xiàn)中所描述�����,可采用標(biāo)準(zhǔn)過程來確定鎖相環(huán)(PLL)中二階環(huán)路濾波器的R0�����、C0 和CP 數(shù)值�����。它采用開環(huán)帶寬(ω0)和相位裕量(?M)作為設(shè)計(jì)參數(shù)�����,并可擴(kuò)展至三階環(huán)路濾波器,從而確定R2 和C2(圖1)�����。該過程可直接解出CP����,然后推導(dǎo)出其余數(shù)值。
2 可能是集成在PLL內(nèi)的固定值元件��,因此僅有R0 和C0 用來控制環(huán)路響應(yīng)��。這便使得上述過程無效��,因?yàn)闊o法調(diào)節(jié)CP���。本文提出一種替代過程,可在CP 數(shù)值固定時(shí)使用�,突破了無法控制CP 值造成的限制。
圖1. 典型二階和三階無源環(huán)路濾波器
假設(shè)條件
本環(huán)路濾波器設(shè)計(jì)方法基于兩個(gè)假設(shè)����,在三階無源濾波器設(shè)計(jì)中,通過調(diào)節(jié)R0 和C0 來補(bǔ)償R2 和C2�����,可以將一個(gè)二階環(huán)路濾波器設(shè)計(jì)擴(kuò)展為三階設(shè)計(jì),此時(shí)通常會(huì)采用這兩個(gè)假設(shè)條件�。
R2 和C2 形成的極點(diǎn)頻率應(yīng)當(dāng)至少比ω0(所需開環(huán)單位增益帶寬)大一個(gè)數(shù)量級;f0 ≤ 0.1/(2πR2C2)��,其中f0 = ω0/(2π)���。
R0-C0-CP 網(wǎng)絡(luò)的R2 和C2 串聯(lián)組合的負(fù)載可忽略不計(jì)��。
二階環(huán)路濾波器的傳遞函數(shù)
二階環(huán)路濾波器有兩個(gè)時(shí)間常數(shù)(T1 和T2)與元件有關(guān):
環(huán)路濾波器傳遞函數(shù)的T1��、T2 和CP 很重要�,因?yàn)樗鼘τ赑LL 的整體響應(yīng)起著很大的作用:
PLL系統(tǒng)函數(shù)
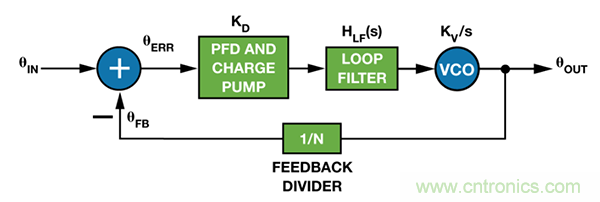
圖2 中的小信號模型為PLL響應(yīng)的等式化提供了一種途徑�����,并為分析輸入端相位干擾所造成的輸出端相位變化提供了模板�����。注意��,壓控振蕩器(VCO)作為一個(gè)頻率源�,表現(xiàn)為理想的相位積分器,因而其增益(KV)系數(shù)為1/s(對積分進(jìn)行等效拉普拉斯變換)。因此�����,PLL的小信號模型是復(fù)頻率s的函數(shù)(s = σ + jω)�。
圖2. PLL小信號模型
PLL的閉環(huán)傳遞函數(shù)(HCL)定義為:θOUT/θIN。開環(huán)傳遞函數(shù)(HOL)定義為:θFB/θIN����,與閉環(huán)傳遞函數(shù)相關(guān)。建議以HOL 來表示HCL��,因?yàn)殚_環(huán)傳遞函數(shù)包含閉環(huán)穩(wěn)定性的線索:
K 表示鑒頻鑒相器(PFD)�����、電荷泵和VCO的組合增益——也就是說�,K = KDKV,其中KD 表示電荷泵電流�,單位為A�����;KV 表示VCO增益����,單位為Hz/V���。HOL、HCL 和HLF 均為s 的函數(shù)�����。等式4 中的負(fù)號表示圖2 中求和節(jié)點(diǎn)的負(fù)反饋導(dǎo)致相位反轉(zhuǎn)���。根據(jù)等式4 定義的HOL導(dǎo)致等式5 中分母的減法運(yùn)算�,直觀地解釋了閉環(huán)穩(wěn)定性��。
檢查等式5�,可以發(fā)現(xiàn)潛在的環(huán)路穩(wěn)定性問題。由于HOL 是復(fù)數(shù)頻率s = σ + jω的函數(shù)��,它必然具有取決于頻率的幅度和相位分量�。因此,對于任意的s 值�����,如果HOL 同時(shí)表現(xiàn)出單位增益和零點(diǎn)相移特性(或2π 弧度的整數(shù)倍)�,則HCL 分母為零�����,閉環(huán)增益再次變?yōu)槲炊x�����,系統(tǒng)變得極不穩(wěn)定����。這意味著穩(wěn)定性受依賴于頻率的HOL 幅度和相位特性所控制�����。事實(shí)上���,在使得HOL 為單位幅度的頻率處�����,HOL 相位必須離開零(或離開2π 任意整數(shù)倍)足夠遠(yuǎn)�����,才能避免等式5 中的分母為零���。
使HOL 為單位幅度處的頻率ω0 非常重要。ω0 處的HOL 相位決定了系統(tǒng)的相位裕量?M��。ω0 和?M 都可由HOL 推導(dǎo)得出�。
根據(jù)ω0 和?M 定義R0 和C0
0 和C0
使用設(shè)計(jì)參數(shù)ω0 和?M 來確定R0 和C0 值要求表達(dá)式包含這四個(gè)變量,以及其它常數(shù)項(xiàng)����。可以從等式4 入手�,因?yàn)榈仁? 定義了HOL。這樣便將HLF 加入其中����,進(jìn)而通過T1 和T2 加入R0 和C0。由于HOL 具有幅度和相位����,因此原則上ω0 和?M 也能加入其中。將等式3 代入等式4����,重新排列各項(xiàng)可得等式6;等式6 以T1 和T2 以及常數(shù)K�、N 和CP 來表示HOL:
將等式3 代入等式4��,重新排列各項(xiàng)可得等式6�;等式6 以T1 和T2 以及常數(shù)K��、N 和CP 來表示HOL:
在s = jω 時(shí)進(jìn)行評估��,可得HOL 頻率響應(yīng)如下:
分母中的(jω)2 項(xiàng)可簡化為–ω2:
HOL 幅度和相位為:
記住�,T1 和T2 是R0、C0 和CP 代數(shù)組合的縮寫表達(dá)式���。ω = ω0 時(shí)評估等式9����,并使|HOL| = 1 即可定義單位增益頻率ω0����,表示HOL 為單位幅度時(shí)的頻率。
類似地�����,ω = ω0 時(shí)評估等式10����,并使∠HOL = ?M 即可定義相位裕量?M���,表示頻率為ω0(單位增益頻率)時(shí)的HOL 相位�����。
擴(kuò)展等式11 和等式12 很容易���,將等式1 中的T2 和等式2 中的T1 代入即可將R0 和C0 帶入等式�。因此���,我們順利地將ω0 和?M 與變量R0 和C0 以及常數(shù)K�����、N 和CP 相關(guān)聯(lián)�����。
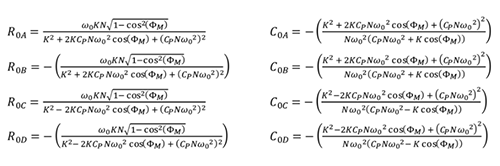
同時(shí)求解我們所得到的等式中的R0 和C0 很困難����。MathCad®提供的符號處理器可求解這兩個(gè)聯(lián)立方程�����,但必須以arctan 代替arccos。進(jìn)行變換后�,符號處理器便可求解R0 和C0,得到下列解集(R0A�、C0A;R0B�����、C0B���;R0C�����、C0C���;以及R0D、C0D)���。有關(guān)對等式12 進(jìn)行變換以便使用arccos 函數(shù)的詳細(xì)信息請參見附錄��。
這個(gè)結(jié)果是有問題的��,因?yàn)槟繕?biāo)是在給定ω0 和?M 的情況下求解 R0 和C0���;而運(yùn)算結(jié)果表明存在四對可能的R0 和C0�,而非唯一的R0�、C0 對���。然而���,若進(jìn)一步檢查這四組結(jié)果,便可得出只有一組解����。
注意,就PLL 建模而言�,上述等式中的所有變量都具有正值,包括cos(?M)��;這是因?yàn)椋?M 的范圍限制在0 和π/2 之間�����。因此,C0A和R0B 顯然是負(fù)數(shù)�����。由此可知�,R0A、C0A 和R0B�����、C0B 可立即加以排除����,因?yàn)樵挡豢赡転樨?fù),但需進(jìn)一步分析R0C����、C0C 和R0D、C0D�����。
注意���,包含R0C���、C0C 和R0D�、C0D 在內(nèi)的四個(gè)等式有公因數(shù):
進(jìn)一步分析可知�,等式13 的形式為:a2 – (2ac)cos(β) + c 2。以b2表示該式����,可得:
等式14 即為余弦定理,以a�、b 和c 表示三角形的三條邊長度,β 表示頂點(diǎn)對邊b 的內(nèi)角�����。由于b2 表示三角形一條邊長度的平方����,它必須為正���,這也就意味著等式14 的等號右邊也必須為正��。因此��,等式13 必須為正����,意味著R0D 的分母為正。R0D 的分子同樣為正���,因此R0D 必須為負(fù)���,這便排除了R0D、C0D�����。這使得僅有R0C����、C0C對可作為等式11 和等式12 的解。
R0 和C0 的限制
雖然等式15 和等式16 有可能是等式11 和等式12 的公共解�����,但它們僅在R0 和C0 均為正時(shí)才有效��。仔細(xì)檢查R0 可知其為正——它的分子為正��,因?yàn)閏os2(x)范圍為0 到1���,且它的分母與等式13相同�,由前文可知其為正。C0 分子同樣與等式13 相同�,因此只要分母滿足下列條件,C0 就為正:
圖3 以圖形方式表示這種關(guān)系����;不等式17 左右兩側(cè)均等于y(藍(lán)色曲線和綠色曲線),水平軸共享ω0 和?M�����。兩條曲線的交點(diǎn)表示ω0 和?M 的邊界����。紅色弧線部分所表示的條件使等式17 成立�����。紅色弧線下方的水平軸部分決定了C0 為正的?M 和ω0 范圍��。注意�����,藍(lán)色曲線和綠色曲線交點(diǎn)正下方水平軸上的點(diǎn)確定了?M_MAX,即?M 的最大值�;該值確保C0 為正。
等式18 要求CPNω02 小于K��,才能滿足?M_MAX 的arccos 范圍為0到π/2 的限制條件�����。這便確定了ω0_MAX���,即ω0 的上限�����,保證C0為正��。
圖3. C0 分母的限制條件
補(bǔ)償R2 和C2(三階環(huán)路濾波器)
就三階環(huán)路濾波器而言��,R2 和C2 分量產(chǎn)生額外的相移Δ?���;該相 移與二階環(huán)路濾波器有關(guān):
為了處理這個(gè)額外的相移,應(yīng)將其從所需的?M 值中扣除���。
將?M_NEW 代入等式15 和等式16 可得到不同的R0 和C0���,然后針對二階解���,將新數(shù)值用來補(bǔ)償R2 和C2 引入的額外相移。R2 和C2 的存在還會(huì)影響?M_MAX�,即?M 的最大允許值。?M 新的最大值(?M_MAX_NEW)為:
結(jié)論
本文演示了僅有R0 和C0 元件值可調(diào)節(jié)時(shí)���,如何使用開環(huán)單位增益帶寬(ω0)和相位裕量(?M)作為二階或三階環(huán)路濾波器的設(shè)計(jì)參數(shù)�����。采用R0 和C0 的二階環(huán)路濾波器仿真PLL����,結(jié)果與HOL 以及由此得到的相位裕量理論值完美吻合�����,從而驗(yàn)證了這些等式����。根據(jù)等式19和等式18�,參數(shù)ω0和?M 針對二階環(huán)路濾波器分別具有上限值���。
確定R0 和C0 的過程中對二階環(huán)路濾波器進(jìn)行了假設(shè),但通過將所需的相位裕量(?M)根據(jù)等式21 調(diào)節(jié)為新的值(?M_NEW)便可擴(kuò)展應(yīng)用到三階環(huán)路濾波器的設(shè)計(jì)中����,進(jìn)而根據(jù)等式22 得到一個(gè)新的上限值(?M_MAX_NEW)。
雖然使用二階環(huán)路濾波器進(jìn)行仿真可驗(yàn)證等式15 和等式16�,但若要驗(yàn)證將設(shè)計(jì)過程擴(kuò)展至三階環(huán)路濾波器的等式則需對環(huán)路濾波器響應(yīng)HLF(s)進(jìn)行重新定義,使其包含R2 和C2���,如下所示:
將HLF 的這種形式應(yīng)用到HOL 和HCL 等式�,便可使用R0 和C0 仿 真三階環(huán)路濾波器設(shè)計(jì)��。對其進(jìn)行仿真可知��,當(dāng)使用三階環(huán)路濾波器時(shí)�����,由理論頻率響應(yīng)和相位裕量推導(dǎo)而得的R0 和C0 計(jì)算值與PLL 的HOL 有關(guān)�。這主要是因?yàn)槭艿搅巳A環(huán)路濾波器中HOL的R2 和C2 影響。
如前所述���,R0 和C0 等式假定為使用二階環(huán)路濾波器���,但在二階濾 波器中不存在R2 和C2���,因此雖然通過調(diào)節(jié)R0 和C0 可以補(bǔ)償R2和C2 造成的相移,但是將它們看做二階環(huán)路濾波器的一部分還是會(huì)構(gòu)成一個(gè)誤差源�。然而,哪怕存在這樣的誤差��,仿真結(jié)果也表明���,使用經(jīng)過調(diào)節(jié)的R0 和C0 值�����,但將ω0 限制在最高為等式19推導(dǎo)結(jié)果的¼也能獲得令人滿意的結(jié)果��。事實(shí)上�,仿真開環(huán)帶寬和相位裕量的結(jié)果表明��,使用三階環(huán)路濾波器的PLL��,其與設(shè)計(jì)參數(shù)(ω0 和?M)的偏差很小�。
仿真結(jié)果
以下為針對三階環(huán)路濾波器PLL 運(yùn)行四次仿真的結(jié)果��。所有仿真均采用下列固定環(huán)路濾波器元件和PLL 參數(shù):
CP = 1.5 nF
R2 = 165 kΩ
C2 = 337 pF
KD = 30 µA
KV = 3072 (25 ppm/V at 122.88 MHz)
N = 100
仿真1 和仿真2 使用ω0 = 100 Hz,該值接近124.8 Hz 的計(jì)算上限值(ω0_MAX)�。因此,仿真1 和仿真2 偏離設(shè)計(jì)參數(shù)值(ω0 和?M)約10%��。另一方面���,仿真3 和仿真4 使用ω0 = 35 Hz����,約為上限值的¼���。與預(yù)期相一致��,仿真3 和仿真4 非常接近設(shè)計(jì)參數(shù)(ω0和?M)����,誤差僅為1%左右���。
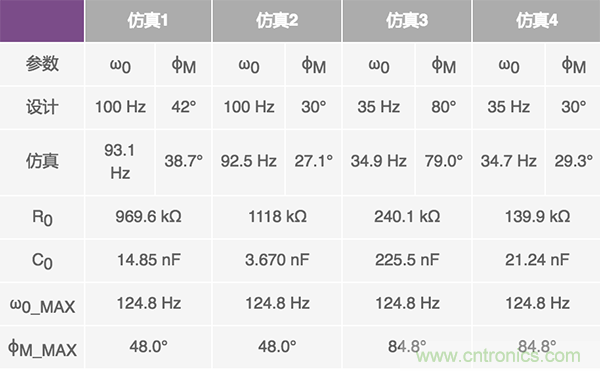
表1 匯總了仿真結(jié)果��,并囊括了給定設(shè)計(jì)參數(shù)ω0 和?M 的R0����、C0、ω0_MAX 和?M_MAX 計(jì)算值��。注意��,為了方便進(jìn)行對比���,建議仿真1和仿真3 都使用?M = 80°�����,但仿真1 必須滿足等式22 的限制條件����,即?M
表1:仿真結(jié)果匯總
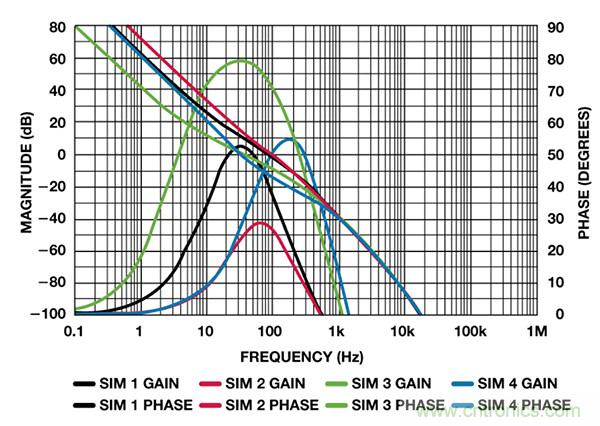
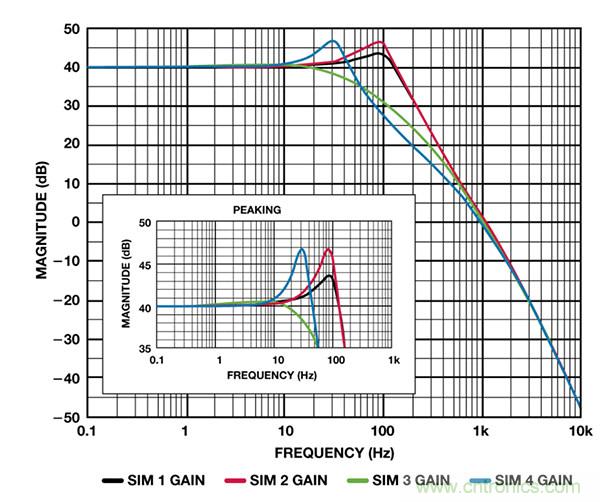
圖4 和圖5 顯示各仿真的開環(huán)和閉環(huán)響應(yīng)��。
圖4. 開環(huán)增益和相位
圖5. 閉環(huán)增益
附錄—將非連續(xù)Arctan 函數(shù)轉(zhuǎn)換為連續(xù)Arccos 函數(shù)
等式10 演示了角度? 等于角度θ2 和角度θ1 之差����,其中θ2 =arctan(ωT2),θ1 = arctan(ωT1)�����。此外,ωT2 可以表示為x/1���;ωT1 可以表示為y/1:
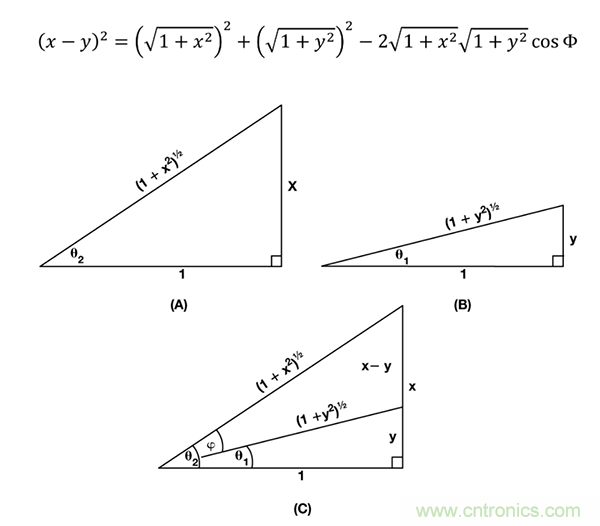
這表明兩者之間存在如圖6 所示的幾何關(guān)系,其中θ1 和θ2 分別由圖6 (b)和圖6 (a)的三角形定義�。圖6 (c)結(jié)合了這兩個(gè)三角形,表示?等于θ1 和θ2 之差��。
余弦定理將三角形的某個(gè)內(nèi)角(θ)與三角形的三條邊(a�����、b 和c)相關(guān)聯(lián)���,關(guān)系式如下:
將余弦定理用在圖6 (c)的? 角,得到:
圖6. 等式10 的幾何表示
求解?:
但是�,由于x/1 = ωT2 且y/1 = ωT1�,因此可用T1 和T2 來表示?�。
參考電路
Brennan, Paul V. 鎖相環(huán):原理與實(shí)踐. McGraw-Hill, 1996.
Keese, William O. AN-1001, National Semiconductor 應(yīng)用筆記, 用于電荷泵鎖相環(huán)的無源濾波器設(shè)計(jì)技術(shù)分析與性能評估. 1996 年 5 月��。
MT-086:鎖相環(huán)(PLL)基本原理
PLL 與集成VCO的PLL
推薦閱讀: